B-Tree 와 B+Tree

개요

B+ 트리는 트리 자료구조 중 하나인 B 트리의 단점을 해소하는 자료구조이다. B 트리에는 이진 트리 중 균형 이진 트리가 사용된다. 따라서 B+ 트리를 알아보기 전에 이진 트리에 대해 먼저 알아보려고 한다.

이진 트리

이진 트리는 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료구조이다.

종류

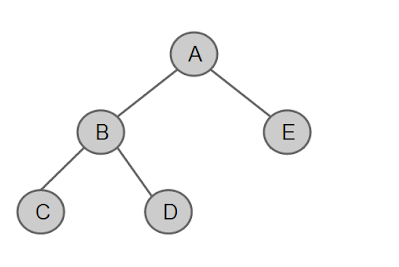
정 이진 트리

: 트리의 모든 노드가 0개 혹은 2개의 자식을 가지는 경우

0개 혹은 2개의 자식을 가지므로 홀수개의 자식을 가질 수 없다.

---

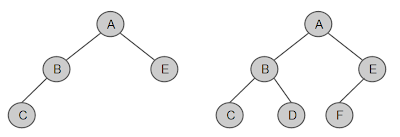
완전 이진 트리

: 마지막 레벨을 제외한 모든 레벨에서 순서대로 (왼쪽부터) 노드가 꽉 채워진 트리

트리를 이용한 검색에서는 완전한 모습에 가까울수록 높은 성능을 낸다고 한다. 그렇기 때문에 데이터를 배치할 때 최대한 완전 이진 트리의 모습과 가깝게 배치하는 것이 좋다.

---

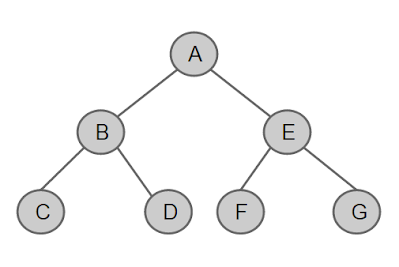
포화 이진 트리

: 리프(Leaf) 노드가 끝까지 꽉 찬 트리

리프 노드를 제외한 모든 노드가 2개의 자식을 가진다. 가장 안정적인 구조이다.

💡 리프 노드? 가장 마지막 노드를 의미

---

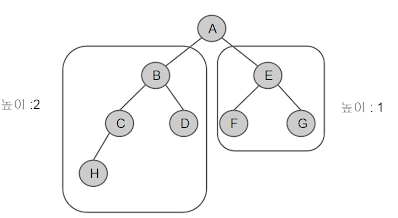
균형 이진 트리

: 리프 노드들의 레벨 차이가 최대 1레벨까지만 나는 트리

균형이 깨질 경우 다시 균형을 유지한다.

B-Tree

B 트리는 균형 이진 탐색 트리의 일종으로 하나의 노드에 많은 정보를 갖고 있다. 또한 이진 트리를 확장해서 삽입과 삭제 시 필요할 경우 스스로 균형을 유지한다. 하나의 노드에 많은 데이터를 가질 수 있다는 장점 때문에, 데이터베이스 시스템의 인덱스 저장 방법으로 많이 이용된다.

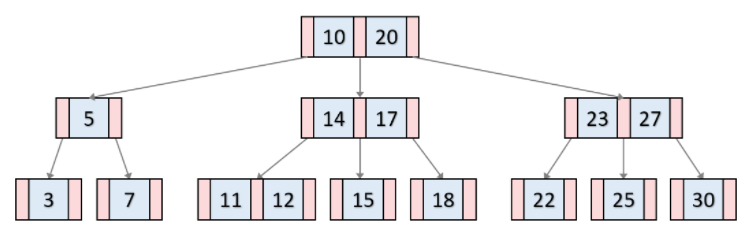
M차 B-Tree

---

한 노드에 M개의 자료가 있다면 M차 B 트리이다. 이 때 자식 노드는 최대 M개이다.

특징

---

✅ 정렬되어 있는 각 노드의 자료

✅ 자료 중복 X

✅ 모든 리프 노드는 같은 레벨

✅ 루트 노드는 적어도 2개 이상의 자식을 가짐

✅ 루트 노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가져야 함

✅ 노드의 자료수가 N이면 자식 수는 N+1 이어야 함

✅ 외부 노드로 가는 경로의 길이는 모두 동일함

B+Tree

B+ 트리는 B 트리의 순차 접근 문제를 개선하기 위해 나온 트리구조로 같은 레벨의 모든 키 값들이 정렬되어 있고 같은 레벨의 형제 노드는 연결 리스트 형태로 이어져 있다. 따라서 특정 값을 찾을 때 리프 노드에 모든 자료들이 존재하고, 연결 리스트로 연결되어 있기 때문에 순차적인 탐색에 유리하다. 따라서 대부분의 데이터베이스 시스템에서는 B+ 트리구조를 사용하고 있다고 한다.

인덱스 노드의 값(value)에는 다음 노드를 가리킬 수 있는 포인터 주소가 존재하고, 데이터 노드의 값에 데이터가 존재한다. 따라서 key는 중복될 수 있고, 데이터 검색을 위해서는 리프 노드까지 내려가야 한다. B 트리에서는 자료의 중복 없이 key가 하나의 노드에만 유일하게 존재했지만, B+ 트리는 노드와 그 외 노드에 공존할 수 있다는 것이다.

💡 인덱스 노드? 리프 노드가 아닌 자료

💡 데이터 노드? 리프 노드 자료

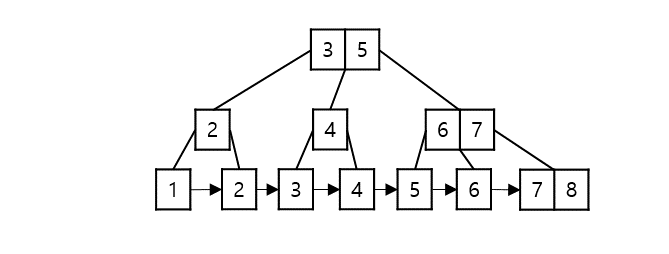
특징

---

✅ (데이터 노드의) 자료 정렬

✅ (데이터 노드에서) 자료 중복 X

✅ 모든 리프 노드는 같은 레벨

✅ 모든 리프 노드는 연결 리스트로 구성

✅ 모든 데이터는 리프 노드에만 존재

✅ 리프 노드에서만 데이터의 삽입, 삭제 연산 발생